The FDA Project Optimus emphasizes that, although precise exploration of safe and efficacious dose is the primary goal of early-phase oncology trials, it is equally important to collect more information on less toxic but still efficacious doses. This broader approach facilitates identification of the optimal biological dose (OBD) rather than the maximum tolerated dose (MTD).
One efficient strategy is the backfill framework, which allows patients to be enrolled at lower doses that have demonstrated safety during the trial. This approach is especially useful when a drug exhibits a non-increasing efficacy pattern, a phenomenon common in modern oncology therapeutics. While the main cohort continues to explore higher doses, additional patients are allocated to previously tested lower doses. This “double-checking” of efficacy at safe doses enables further information accumulation for more reliable dose selection.
A key challenge, however, is that backfill cohorts are enrolled after the main cohort. As a result, pending dose-limiting toxicity (DLT) responses in backfill cohorts may delay the continuous enrollment of main cohorts. In other words, pending outcomes cannot be directly incorporated into statistical inference or the dose escalation algorithm, even though the trial could otherwise have proceeded without the backfill cohorts.
Then, how to make a backfill trial smoother and efficient? Considering that blindly pausing can disrupt a trial process, Bi3+3 (?) applies the probability of decision (POD) framework, which quantifies the probability of making each dose decision based on pending DLT outcomes. This innovation allows the trial to pause only when necessary, thereby maintaining efficiency while still protecting patient safety.
Denote “main cohort” (mc) the cohort of patients that drives dose escalation, and “backfill cohort” (bc) the cohort of patients for backfill at lower doses. The algorithm proceeds as follows:
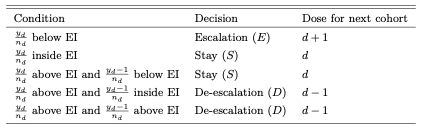
(1) Main Cohort Enrollment: a trial begins by enrolling an mc of patients at dose d, and the temporary dosing decision 𝒮d ∈{E,S,D} is obtained using the i3+3 design (?) (See the table below).

(2) Backfill Cohort Enrollment: Once the mc is assigned, bc enrollment begins. Patients are randomly assigned to backfill doses lower than the current dose: ℬd = {k0,k0 + 1,...,d − 1}.
How are backfill doses determined? For trial efficiency, doses that exhibit too low efficacy will be excluded during the trial. In other words, the lowest backfill dose k0 is refreshed. For each candidate dose k ∈ℬd, compute the expected efficacy response rate at higher doses k+,
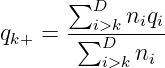
Using MCMC samples of qi∣data ∼ Beta(α0,β0), compute the posterior probability ξk = Pr(qk+ > qk∣data) to compare with a prespecified threshold ξ0, say ξ0 = 0.8. If ξk > ξ0, dose k is deemed less efficacious, and k0 is updated to k + 1.
If any backfill patients have pending DLT outcomes, apply POD-i3 to decide whether to suspend the trial.
What is POD-i3? It is a framework that considers probability of making a dose decision, where the randomness is induced by the uncertainty in the pending DLT outcomes. Let yk,obs denote the observed toxicity outcomes at a backfill dose k, and Y k,mis is the unobserved DLT outcomes, which is a random variable. 𝒜k = 𝒜k[(yk,obs,Y k,mis),nk] ∈ {−1, 0, 1} represents the decision function at dose k to de-escalate (D), stay (S), and escalate (E), respectively, based on i3+3. The POD method calculates the posterior probabilities of each dosing decision a at dose k:
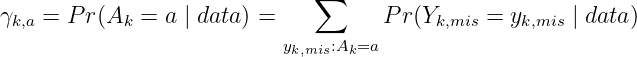
(3) Informing the Next Main Cohort: once pending outcomes in bc are resolved, a dosing decision for mc will be informed by backfill decisions 𝒯k, which is based on POD-i3 described above:
(4) Repeat: with the assistance of several safety rules, repeat the above process until the main cohort reaches the maximum sample size or all doses have been tested.
At the end of the trial, similar to many existing designs, Bi3+3 applies the pooled adjacent violators algorithm (PAVA) to the posterior mean toxicity probabilities for all doses to resolve tied dose issues. Among all tested doses, select the MTD that satisfies

To determine the OBD, Bi3+3 modifies ? and constructs a four-parameter model for the dose-efficacy relationship. For the probability of efficacy qd, assume
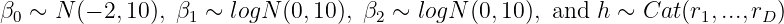
Here, rd is small (e) for doses with no patients, and otherwise distributed evenly across tested doses:
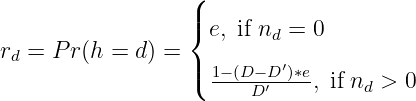
where D′ is the number of doses with enrolled patients. We can use the efficiency data 𝒟 = {(vd,nd),d = 1,...,D} to calculate the posterior probability of dose d being the change point ϕd = Pr(h = d∣𝒟). The estimated change point h∗ is the dose that has the highest ϕ d or D′.
In the end, compared with the dose obtained from MTD selection, the final OBD is
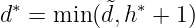
In words, select either the first plateau dose or the MTD dose, whichever is lower.
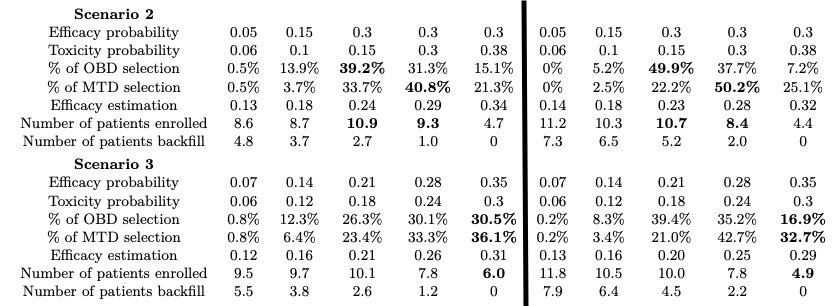
The authors compared Bi3+3 against the Backfill CRM design (?) under five distinct scenarios, and two of the results are shown in Figure 1.
In addition, another key feature of Bi3+3 is its efficacy estimation. We can see that estimated efficacy response rates in general do not deviate much from the true probabilities.
The Bi3+3 design was also compared with mTPI-2 (?), a design that does not allow backfill. The results show that Bi3+3 has a much shorter trial duration and assigns patients to lower doses, gathering more patient information.
Key advantages of Bi3+3: